Gradient, Divergence and Curl...as plumbing [6.G]

See Strang, section 6.5, Divergence and Curl

Let's imagine the vectors $\myv F(\myv r)$ in a vector field in multiple dimensions as representing water flow.

• Gradient, $\myv \grad$: Which way does water flow in a landscape (=surface)?
• Curl, $\myv \grad \times$: Any swirling happening?
• Divergence, $\myv \grad \cdot$: Where are the leaks or faucets?

To a good approximation, water is an incompressible fluid. This means:

• Even if the pressure changes, 1 gallon of water will keep the same volume and the same density.
• If we put one gallon of water per minute into one end of a pipe of constant diameter, then we expect one gallon per minute to flow out of the other end.
• If less than one gallon per minute flows out the other end, then we can be certain that there must be a leak somewhere in the pipe.
  
  Flickr user Ibai

Gradient and the "nabla" _operator_

[The following ideas will be illustrated with functions of 2 variables, but can be extended to 3 or more variables.]

Consider a function which represents the height, $h(x,y)$, of a surface. The gradient of $h$: $$\myv\grad h =h_x \uv i +h_y \uv j,$$ points in the steepest "uphill" direction for the landscape $h$: If water is released at $(x,y)$ it should start flowing in the $-\myv \grad h$ direction.

Re-arranging how the gradient is written: $$\myv \grad h=\uv i \frac{\del}{\del x}h + \uv j \frac{\del}{\del y}h=\left[\uv i \frac{\del}{\del x} + \uv j \frac{\del}{\del y}\right] h,$$ suggests the idea of the *thing* in [...] "operating" on the scalar function, $h$, to produce the gradient vector field. This operator is called...

The nabla operator: $$\myv \grad \equiv \uv i \frac{\del}{\del x} + \uv j \frac{\del}{\del y}.$$

• It's a vector operator.
• When nabla operates on a scalar function, $h$, it produces a vector field: the gradient field. $$\begineq \myv \grad h(x,y) &= \left[\uv i\,\frac{\del }{\del x}+\uv j\,\frac{\del }{\del y}\right]h(x,y)\\ &= \frac{\del h}{\del x}\,\uv i+\frac{\del h}{\del y}\,\uv j \equiv\color{blue}\langle h_x, h_y\rangle.\endeq$$

The Curl

The cross-product-like object involving $\myv \grad$ and a vector field $\myv F=P(x,y,z)\uv i+Q(x,y,z)\uv j + R(x,y,z)\uv k$ is

The curl of a vector field $\myv F$ is: $$\begineq\myv \grad \times \myv F &= \begincv \uv{i}& \uv{j}& \uv{k}\\ \frac{\del}{\del x} & \frac{\del}{\del y} & \frac{\del}{\del z}\\ P& Q& R\endcv \\ &= \uv{i}\left(\frac{\del R}{\del y}-\frac{\del Q}{\del z}\right) + \uv{j}\left(\frac{\del P}{\del z}-\frac{\del R}{\del x}\right) +\uv{k}\left(\frac{\del Q}{\del x}-\frac{\del P}{\del y}\right)\endeq.$$

If $\myv F$ is a function of only $x$ and $y$, then only the $\uv k$ component is non-zero.

For $\myv F(\myv r) = -y \uv{i} +x \uv{j}$, sketch $\myv F$ in the $x-$, $y-$ plane ($z=0$)...

$$\myv \grad \times \myv F = \begincv \uv{i}& \uv{j}& \uv{k}\\ \frac{\del}{\del x}&\frac{\del}{\del y}&\frac{\del}{\del z}\\ -y& +x& 0\endcv = 2\uv{z}.$$

For this function, notice that the curl has the same value everywhere, not just at the origin.

In terms of vector field limited to two dimensions, $\myv F=P(x,y)\uv i+Q(x,y)\,\uv j$, in which there is no $R$, $$\myv \grad \times \myv F = \frac{\del Q}{\del x}-\frac{\del P}{\del y}.$$

You should be able to "eyeball" the sign of the curl at a point by looking at the difference: $$\begineq &\ \ \text{change of the $y$-component of $\myv F$ as}\ x\uparrow^+ \\ -&\ \ \text{change of the $x$-component of $\myv F$ as}\ y\uparrow^+ \endeq $$

"Swirliness" defined by a paddle-wheel

Again thinking of $\myv F$ as the field specifying water velocity...

Imagine placing a paddle-wheel with axis oriented in the $\uv{k}$ direction in the water flow represented by the vector function $\myv F$ and seeing whether it turns counter-clockwise (positive curl) or clockwise (negative curl).

In a 3-d water flow field, we could also try orienting the paddle wheel towards $\uv{j}$ or $\uv{k}$ to check for components of the curl in all possible directions.

Conservative fields and curl

We saw that fluid flow in a landscape is related to the gradient field.

Can you imagine some kind of landscape/surface that would give rise to this flow?

Howzabout this landscape?...

Or this somewhat more realistic one?...

Curl of a gradient

If our vector field $F$ is the gradient of a potential function, then we have $\myv F=\myv \grad f = \langle f_x,f_y\rangle$. The curl of this two-d vector field would be $$\myv \grad \times \langle f_x,f_y,0 \rangle = \begincv \uv{i}& \uv{j}& \uv{k}\\ \frac{\del}{\del x}&\frac{\del}{\del y}&\frac{\del}{\del z}\\ f_x& f_y& 0\endcv = \left( f_{yx}-f_{xy} \right)\uv{z}.$$ So, by Clairault's Theorem, this must be 0 for a smooth, continuous function $f(x,y)$. More generally, even in 3-d:

If $f$ is a scalar function of 3 variables, that has continuous second-order partial derivatives, then $$\myv \grad \times (\myv \grad f) = 0$$ at all points $(x,y,z)$.

Alternative statements:

• Any swirliness in the flow $\myv F$? Sorry, there's no landscape for which $\myv F$ represents the flow. (There's no potential function, $h$.)
• A vector field $\myv F$ is conservative if, and only if, $\myv \grad\times \myv F=0$.

This is a test we can use on any vector field $\myv F$ to decide whether it's worth looking for a potential function or not!

A field $\myv F$ is said to be irrotational if for all points in space: $$\myv \grad \times \myv F=0$$

The Divergence

We could form a dot product between the nabla vector operator and...

a vector field, $\myv F(x,y)=P(x,y)\uv i +Q(x,y)\uv j$, where $P$ is the $x$-component of $\myv F$.

The dot product of two vectors is a scalar. This defines...

The divergence of $\myv F(x,y)$ is $$\begineq \myv \grad \cdot \myv F &= \left(\uv{i} \frac{\del}{\del x} +\uv{j} \frac{\del}{\del y}\right) \cdot \left( P\uv{i} + Q\uv{j}\right)\\ &=\frac{\del P}{\del x} + \frac{\del Q}{\del y}.\endeq$$

For the following sketches of 2-dimensional vector fields, $\myv F(x,y)$, what [pos, neg or 0] is the 2-d divergence, $\frac{\del P}{\del x}+\frac{\del Q}{\del y}$ at the positions marked in purple?

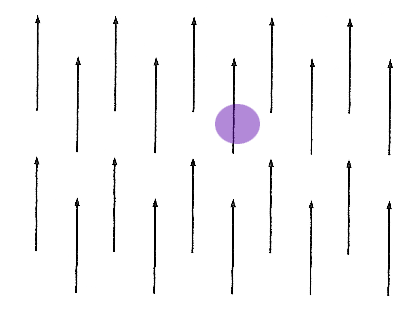
$\myv F(x,y)=3\, \uv j$

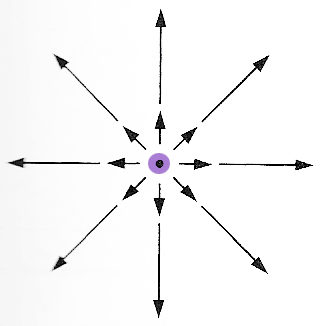
$\myv F(x,y)=x\uv i +y\uv j$

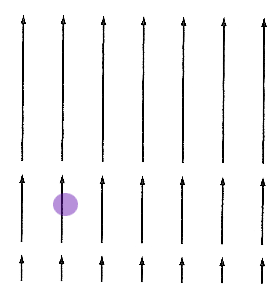
You can estimate visually, without a formula... For the vector field above:

Estimating the divergence of a vector field - Narrated: 2 min.

Where are the leaks (or faucets)?

Imagine that the arrows, $\myv F(x,y)$, represent the velocity of 2-d flow of an incompressible fluid (water!).

Now imagine injecting a "cloud" of purple dye at a location you'd like to investigate for "leaks" in your system, places where the water is disappearing.

A place where the cloud gets smaller corresponds to a location where the divergence is negative: a "leak" (or sink, or drain) where water is leaving your 2-d system

...leaving your 2d system **into another dimension**!

Places where the cloud gets bigger have positive divergence. There must be a "source" (or faucet) of water **from another dimension**(!).

Consider again these vector fields, as if $\myv F$ of water flow... What's happening to the size of the purple spot?

Divergence means...

Incompressible flow in 2-d means $$\myv \grad \cdot \myv F = 0$$ **unless** there are sources (or sinks) bringing in more water from (or taking away some to) "another dimension".

When the fluid flow is incompressible, then, if the vectors represent water flow, just as much water enters any bounded volume (or area in 2d) as exits the volume, **unless** (see above).

$\myv F(x,y)=3\, \uv j$

$\myv F(x,y)=x\uv i +y\uv j$

Electric fields The divergence of the electric field in empty space is zero. Any divergence of the electric field must be due to electric charge. So, we say $\myv \grad \cdot \myv E(x,y,z) \propto \rho(x,y,z)$, where $\rho$ is the charge density. This statement is equivalent to saying: Charges are the sources or sinks of the electric field.

• MathInsight.org: the divergence idea.

In the /mvhandouts/ folder... 06.5.VisualDivCurl.php