Vector fields
From now on, we'll be using Gilbert Strang's, Calculus Vol 3 textbook. Chapter 6 is the beginning of his Vector Calculus section.
2D vector field
Examples
$$\myv F(x,y)=-y\uv i +x \uv j$$
Examples
Examples
To do /mvhandouts/
- 06.1.VectorFieldSketches - Vector Field Sketches by hand
3D vector field
Examples
Examples
$$\myv F(x,y,z)=z\uv k$$
Mathematica
Download and open "13.1.MticaVectorFields.nb" in the handouts folder...
- VectorPlot - 2D vector fields
$$\myv F(x,y)=y\uv i -x\uv j$$
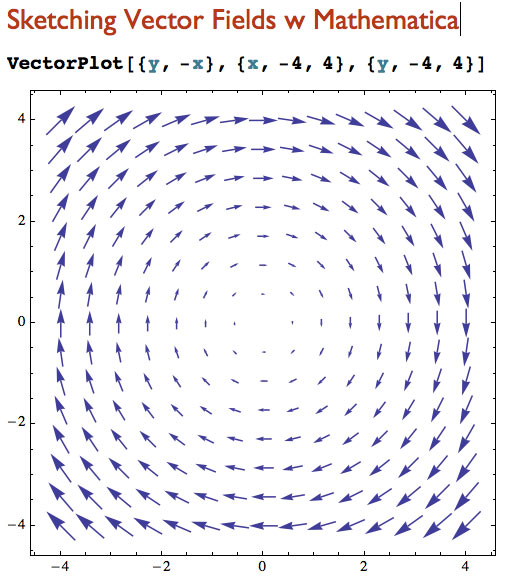
- VectorPlot3D - 3D vector fields
$$\myv F(x,y)=y\uv i+z\uv j+x\uv k$$
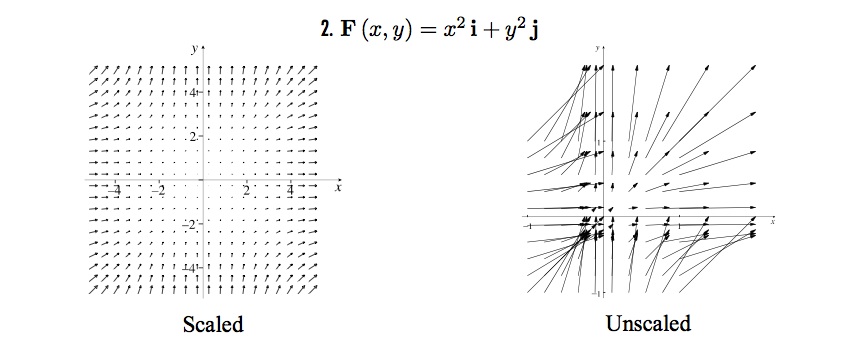
Use VectorScale $\to$ Automatic if necessary.
To Do
See the Jupyter notebook "vector fields" in your handouts folder on cocalc.com for examples of how to make plots of vector fields in CoCalc.
Sketch these in CoCalc
- $\myv F(x,y)=x^2 \uv i +x^3 \uv j$
- $\myv F(x,y)=y^3 \uv i +y^2 \uv j $
- $\myv F(x,y)=(x+y) \uv i +(x-y) \uv j$
- $\myv F(x,y,z)=y \uv i + z \uv j + x \uv k$
- $\myv F(x,y,z)=y\uv i -2 \uv j +x \uv k$
- $\myv F(x,y,z)=1\uv i -y^2 \uv j +z\uv k$
